การจะเข้าใจ Hidden Markov Model ได้ จำเป็นที่จะต้องศึกษา Markov Model ก่อน ซึ่งการศึกษา Markov Model มันก็เหมือนกับการดูละคร คือมันมีตัวละครหลายตัว แต่ล่ะฉากก็จำเป็นที่จะต้องเดินเรื่องเพื่ออธิบายตัวละครแต่ล่ะตัว ทีนี้ผู้จัดทำละครเขาก็ไม่มีปัญญาจะปูพื้นตัวละครแต่ล่ะตัวพร้อม ๆ กันให้เราดูได้ เพราะพวกเราไม่ได้ดูทีวีที่มีหลายหน้าจอพร้อม ๆ กันแบบ CCTV ที่จะมีภาพของตัวละครแต่ล่ะตัวออกมาโลดแล่นให้เห็นพร้อม ๆ กัน ดังนั้น สิ่งที่ผู้จัดทำละครจะทำก็คือ การทยอยอธิบายตัวละครทีล่ะตัว ทีล่ะฉาก แบบเป็นลำดับ จากนั้น จึงตัดฉากไปมาระหว่างแต่ล่ะเหตุการณ์ของตัวละคร ทำให้คนดูไม่รู้สึกสะดุดไหลลื่น และมีความเข้าใจในตัวละครแต่ล่ะตัวได้
การเข้าใจ Markov Model เองก็เช่นเดียวกัน เพราะผู้อธิบายมักจะใช้วิธีการเล่าเรื่องตัดฉากไปมา ระหว่างตัวโมเดล, ไดอะแกรม, ตัวอย่าง และ สมการคณิตศาสตร์ จึงทำให้บางครั้งถ้าเราตามไม่ทัน เราอาจจะงงได้
มายกตัวอย่าง Markov Model อย่างง่ายกันดีกว่า นั่นคือ Model ของความน่าจะเป็นในการโยนเหรียญหนึ่งเหรียญ โดยมีสถานะที่เป็นไปได้สองสถานะคือ หัว และ ก้อย
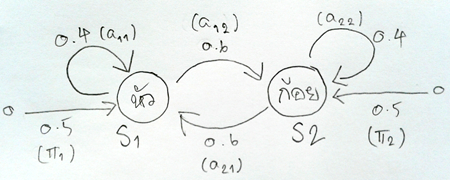
Markov Model มีสมมติฐานที่ว่า ความน่าจะเป็นของสถานะปัจจุบัน จะขึ้นกับความน่าจะเป็นของสถานะก่อนหน้า ดังนั้น ก็เลยมีการวาดความหมายออกมาแบบภาพที่ 1 ซึ่งถ้าเป็นคนมีพื้นฐานก็จะเข้าใจได้อย่างลาง ๆ ว่ามันมีการเคลื่อนผ่านอย่างสัมพันธ์กัน, มีการให้ค่าน้ำหนักกับการเคลื่อนผ่าน และ มีการแทนโน่นนี่นั่นด้วยตัวแปรสองมิติ เป็นต้น
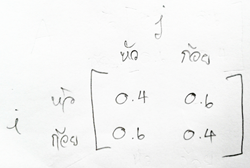
ถ้าเราเอาภาพที่ 1 มาทำเป็น Matrix เราก็จะได้เป็นภาพที่ 2 เป็นการย่อภาพแบบ Model ให้กลายเป็นแบบ Matrix ซึ่งจะดูง่ายต่อความเข้าใจมาก ๆ
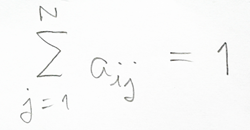
แต่ถึงกระนั้น ก็ยังจำเป็นที่จะต้องอธิบายให้เป็นสมการตามภาพที่ 3 เพื่ออธิบายให้เข้าใจว่า แต่ล่ะแถวของแนวนอนใน Matrix เมื่อบวกรวมกันแล้วต้องได้ค่าเท่ากับ 1 หรือก็คือ ความน่าจะเป็นของการเคลื่อนออกจากสถานะปัจจุบันไปยังสถานะหลาย ๆ อันที่เป็นไปได้ทั้งหมด รวมกันยังไงก็ต้องเท่ากับ 1
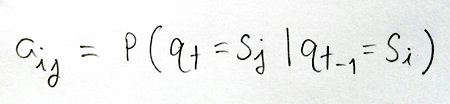
และยังต้องใช้สมการเพื่ออธิบายในภาพที่ 4 เพื่อให้เข้าใจว่าความน่าจะเป็นของแต่ล่ะเส้นทางมันมาได้ยังไง ซึ่งอ่านแล้วก็ดูเข้าใจยากมาก แต่แปลได้ง่าย ๆ ว่า ความน่าจะเป็นจะเกิดขึ้นได้ ต่อเมื่อมีการเคลื่อนจากสถานะหนึ่งไปยังอีกสถานะหนึ่งนั่นแหล่ะ
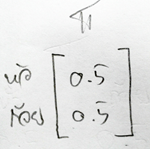
แต่กระนั้นก็ตาม สมมติฐานของ Markov Model ที่ว่า ความน่าจะเป็นของสถานะปัจจุบัน จะขึ้นกับความน่าจะเป็นของสถานะก่อนหน้านั้น มันยังไม่ถูกทั้งหมด เพราะต้องไม่ลืมว่าทุกอย่างมันต้องมีการเริ่มต้น ดังนั้น เราจำเป็นจะต้องคำนึงความน่าจะเป็นของสถานะแรกที่เป็นสถานะตั้งต้นก่อน ซึ่งเป็นสถานะหยุดนิ่ง และไม่ได้เคลื่อนไปยังสถานะอื่นใดเลย โดยการทำความเข้าใจด้วย Matrix แบบภาพที่ 5
ทีนี้เมื่อเราได้ Model เอย สมการเอย และ Matrix เอยมาเรียบร้อยแล้ว จากนั้นเราก็จำเป็นที่จะต้องมาเข้าใจถึง “ความเป็นไปได้” ในการเกิด “ความน่าจะเป็น” อีกทีนึง
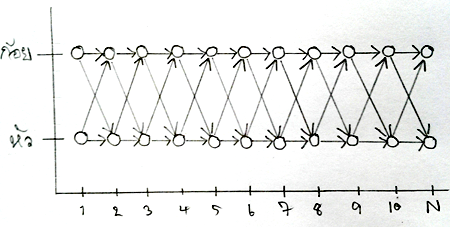
จากภาพที่ 6 ซึ่งถูกเรียกด้วยศัพท์เทคนิคว่า Trellis Diagram เผยให้เราเห็นว่า ในแต่ล่ะครั้งที่เราโยนเหรียญ มันมี “ความเป็นไปได้” ทั้งหมดในเส้นทางที่จะเกิด “ความน่าจะเป็น” ยังไงบ้าง ซึ่งภาพที่ 6 นี้สอดคล้องกับภาพที่ 1 คือ ภาพที่ 1 อธิบายในแง่ของการไหลเวียนแบบหยินหยาง ในขณะที่ภาพที่ 2 อธิบายในแง่ของการไหลเวียนตามแกนเวลา
สุดท้าย เมื่อเราเข้าใจในการไหลเวียนแบบหยินหยาง และ เข้าใจในการไหลเวียนตามแกนเวลาแล้ว เราก็จะมาจบที่สมการคณิตศาสตร์ง่าย ๆ ตามภาพที่ 7
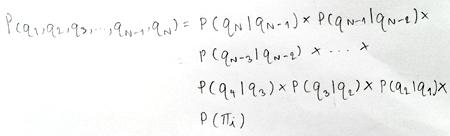
สมการในภาพที่ 7 ได้อธิบายถึง “ความเป็นไปได้” ที่จะเกิด “ความน่าจะเป็น” ตาม Trellis Diagram ในภาพที่ 6 ซึ่งสมการนี้ดูแล้วปวดกบาลมาก แต่สามารถแปลได้ใจความง่าย ๆ ว่า ถ้าอยากรู้ความน่าจะเป็นของสถานะปัจจุบัน ก็เอาความน่าจะเป็นของสถานะก่อนหน้าซึ่งเป็นไปได้ทั้งหมดมาคูณกันซะ (หรืออาจะมีบวกด้วยถ้าจำเป็น) แล้วพอคำนวณกันเสร็จแล้วก็ไปคูณกับสถานะตั้งต้นนู่น แค่นี้ก็จะรู้ความน่าจะเป็นของสถานะปัจจุบันแล้ว
สรุปที่อยากจะบอกก็คือ อ่านพวกนี้ต้องมองให้เหมือนดูละคร มันมีตัดฉากไปมาหลายที ต้องอ่านแล้วเข้าใจตามมันทัน

