ยกตัวอย่าง ทฤษฎีบทของเบย์

ทฤษฎีบทของเบย์เป็นทฤษฎีความน่าจะเป็นเชิงอนุมานที่ถูกใช้กันอย่างกว้างขวางในงานคอมพิวเตอร์ชั้นสูงครับ ไม่ว่าจะเป็นการรู้จำแบบมีผู้สอนเชิงเส้นด้วย Naive Bayes หรือ การรู้จำเสียงพูดด้วย Hidden Markov Model หรือ การคำนวณสภาวะ Superposition ของคิวบิตในควอนตัมคอมพิวเตอร์ ก็ล้วนตั้งอยู่บนหลักการของทฤษฎีบทของเบย์ทั้งนั้น

โดยหน้าตาของสมการตามทฤษฎีบทของเบย์ก็เป็นแบบข้างล่างนี้

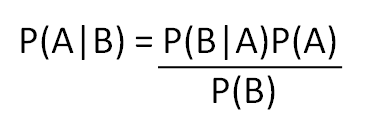
จริง ๆ แล้วทฤษฎีบทของเบย์ก็สืบต่อมาจากทฤษฎีความน่าจะเป็นแบบมีเงื่อนไขอีกทีนึงน่ะครับ เป็นโมเดลที่อธิบายว่าความน่าจะเป็นในลำดับถัดไปจะขึ้นกับความน่าจะเป็นของลำดับก่อนหน้า อะไรประมาณนั้น

ซึ่งถ้าจะคำนวณความน่าจะเป็นของลำดับถัดไปโดยขึ้นกับความน่าจะเป็นของลำดับก่อนหน้า ก็สามารถทำได้ง่าย ๆ ตามสมการข้างล่างนี้ครับ

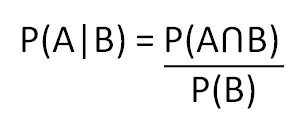
แล้วในเมื่อมันมีสมการง่าย ๆ อยู่ก่อนแล้ว ทำไมเรายังต้องคำนวณโดยใช้ทฤษฎีบทของเบย์อีก???

คำตอบคือ บางครั้งการคำนวณความน่าจะเป็นของลำดับถัดไป โดยขึ้นกับความน่าจะเป็นของลำดับก่อนหน้า มันทำแบบตรงไปตรงมาไม่ได้ครับ มันต้องทำแบบอ้อม ๆ ดังนั้น ทฤษฎีบทของเบย์เลยเป็นสิ่งที่แก้ปัญหาในเรื่องนี้ไปโดยปริยาย

ก่อนอื่น ยกตัวอย่างข้อมูลให้ดูแล้วกันครับ ตามตารางด้านล่างนี้ เป็นข้อมูลคุณสมบัติของบุคคลที่มีเพียง 5 คนเท่านั้น โดยคุณสมบัติของคนเหล่านั้นก็คือ หน้าตา รูปร่าง เส้นเสียง การแสดง และ อาชีพ ครับ

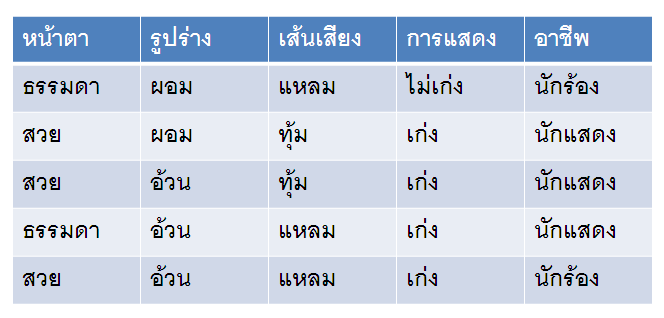
ทีนี้จะตั้งโจทย์ครับ โจทย์คือให้หาว่าความน่าจะเป็นที่บุคคลในข้อมูลตัวอย่างจะเป็นนักแสดงและเป็นคนรูปร่างผอม ซึ่งถ้าหาโดยใช้สมการตามความน่าจะเป็นแบบมีเงื่อนไข ก็จะได้ตามสมการด้านล่างนี้

คำตอบคือ 1 ส่วน 2 ซึ่งแบบข้างบนนี้ตรงไปตรงมา แต่ถ้าหาโดยใช้ทฤษฎีบทของเบย์บ้างล่ะจะเป็นยังไง? ซึ่งก็เป็นไปตามด้านล่างนี้

จะเห็นว่าคำตอบที่คำนวณได้ตามทฤษฎีบทของเบย์ มันก็เหมือน ๆ กับคำตอบที่คำนวณได้ตามทฤษฎีความน่าจะเป็นแบบมีเงื่อนไขนั่นแหล่ะครับ แล้วในเมื่อคำตอบมันเหมือนกัน แล้วเราจะไปใช้ทฤษฎีบทของเบย์ทำไมอีก???

คำตอบก็เพราะว่า ในสถานการณ์จริง เราอาจไม่สามารถหาความน่าจะเป็นแบบมีเงื่อนไขอย่างตรงไปตรงมาได้ครับ บางครั้งมันยอกย้อน มันต้องอ้างอิงกลับไปกลับมาถึงจะหาคำตอบได้ ดังนั้น ด้วยคุณสมบัติของทฤษฎีบทของเบย์ ก็เลยทำให้มันกลายเป็นเครื่องมือที่นิยม สำหรับงาน Machine Learning, Data Mining หรือ Quantum Computing ไปโดยปริยายนั่นเอง